Appendix B

Click image for larger version

---

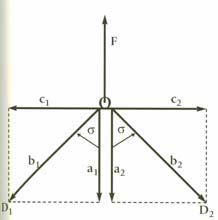
If O is a point is space representing the sphincter, a force F, representing the tension applied to it by LM contraction, will be opposed in the plane by the phrenoesophageal ligaments represented by the two vectors b₁ and b₂ . The projections of b₁ and b₂ on the vertical are a₁ and a₂. The vertical components are both in the opposite direction to F and counteract its tendency to elevate point O. In the same way, c₁ and c₂ are the projections of b₁ and b₂ in the horizontal direction.

From the geometry we can write:

a₁ = b₁ cos sigma
a₂ = b₂ cos sigma

c₁ = b₁ sin sigma
c₂ = b₂ sin sigma

a₁ = a₂

c₁ = -c₂

The sum of the a₁ and a₂ vectors will prevent upward translation of point O. The effect of the c₁ and c₂ vectors, which are of opposite sign, will be to pull point O in opposite directions.

If O, instead of being a point, is a minute annulus representing the inner surface of a closed sphincter, the effect of the c vectors will be to separate the opposite walls. If the whole diagram is rotated about the vertical axis distributing these vectors in 3 dimensions, all of the periphery of the closed sphincter will be spread open without any lateral translation of the sphincter itself.

The detailed distribution is extremely difficult to model mathematically because the diaphragm, the esophagus and the PEL are all elastic, not rigid structures. Because of this, point O is elevated as the PEL stretches and the angle changes. Nevertheless, it is clear that the pull of the contraction LM will have two effects: 1.) It will open the sphincter and 2.) It will stretch the PEL producing a "sliding hiatus hernia."

If equivalent force is applied at the endpoints of the PEL, D₁ and D₂ by the diaphragmatic contraction of a hiccup, the resulting distribution of forces will be identical. Thus a hiccup is the mechanical equivalent of a contraction of the LM and has the same effect in releasing the sphincter.The PEL is essential to this force resolution. When it ruptures, reflux is alleviated.

BACK