Appendix A
When a hollow organ is distended, its thin mucosal layer has a maximum circumference. The cross sectional area of the lumen
is also maximal. When the organ contracts, the area of the lumen decreases to zero. The circumference, however, cannot
approach zero as the elasticity of the mucosa is not infinite. We can get a numerical handle on these circumstances by
noting that the area of the mucosal layer remains constant despite distention or collapse of the lumen.
If one assumes that as much mucosa is squeezed into a given cross section as is squeezed out, then the cross sectional area of the mucosal layer
will be the same before and after contraction of the gut. Before contraction (Figure 1) the mucosal area is the difference between the areas of
the inner and outer
circles:
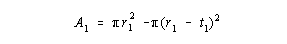 |
After contraction (Figure 2) the mucosal area is . . . |
| As the mucosal area is unchanged by contraction, these expressions can be set equal to each other and solved for r2 resulting in the expression . . . |
|
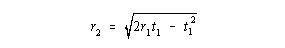 |
The circumference of the free margin of the mucosa after contraction, C2, is a fraction of its pre-contraction length. The decimal fraction C2/C1 is equal to E, the elasticity of the mucosal tissue. It is the elasticity which determines how much the mucosa can shrink. The fully contracted circumference, in leiu of shrinking to zero, must form folds. |
From Figure 3, the mucosal length taken up by one fold is twice the distance from the center of the organ to the depth of the interfold valley or . . .
| An expression for Nf, the expected number of post-contraction folds, can now be written. | |
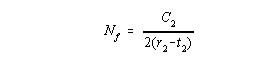 |
The dimensions are all post-contraction, however, from the above, we know that C2 = C1E and , from Figure 1, C1 = 2(r1-t1). Moreover, r2 was calculated in equation 3. We can also calculate that t2 C2 = t1C1 or |
| Performing the indicatedsubstitutions yields a formula for fold numbers
in terms of the inital values of thickness, organ radius and mucosal elasticity.
The subscripts, therefore, can be dropped giving . . . |
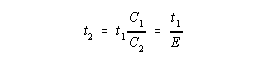 |
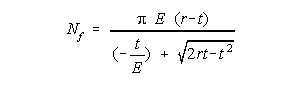
Last Updated July 31 2007 by David PJ Stiennon